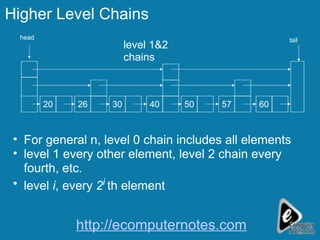
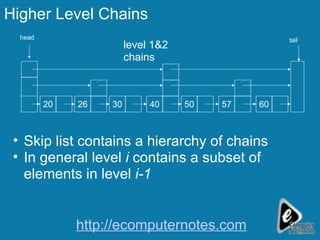
The document discusses different data structures for storing and searching data, including binary search, arrays, linked lists, and skip lists. Binary search is an efficient search algorithm that divides a sorted array in half at each step to search for a target value. Skip lists are a probabilistic data structure that allow for faster search times than linked lists by maintaining multiple levels of sorted lists that skip over elements.

1. Class No.33 Data Structures http://ecomputernotes.com

2. Searching an Array: Binary Search Binary search is like looking up a phone number or a word in the dictionary Start in middle of book If name you're looking for comes before names on page, look in first half Otherwise, look in second half http://ecomputernotes.com

3. Binary Search If ( value == middle element ) value is found else if ( value < middle element ) search left-half of list with the same method else search right-half of list with the same method http://ecomputernotes.com

4. Case 1: val == a[mid] val = 10 low = 0, high = 8 5 7 9 10 13 17 19 1 27 1 2 3 4 5 6 7 0 8 a: low high Binary Search mid mid = (0 + 8) / 2 = 4 10 http://ecomputernotes.com

5. Case 2: val > a[mid] val = 19 low = 0, high = 8 mid = (0 + 8) / 2 = 4 Binary Search -- Example 2 5 7 9 10 1 13 17 19 27 1 2 3 4 5 6 7 0 8 a: mid low high new low new low = mid+1 = 5 13 17 19 27 http://ecomputernotes.com

6. Case 3: val < a[mid] val = 7 low = 0, high = 8 mid = (0 + 8) / 2 = 4 Binary Search -- Example 3 10 13 17 19 5 7 9 1 27 1 2 3 4 5 6 7 0 8 a: mid low high new high new high = mid-1 = 3 5 7 9 1 http://ecomputernotes.com

7. val = 7 Binary Search -- Example 3 (cont) 5 7 9 10 13 17 19 1 27 1 2 3 4 5 6 7 0 8 a: 5 7 9 10 13 17 19 1 27 1 2 3 4 5 6 7 0 8 a: 5 7 9 10 13 17 19 1 27 1 2 3 4 5 6 7 0 8 a:

8. Binary Search – C++ Code int isPresent(int *arr, int val, int N) { int low = 0; int high = N - 1; int mid; while ( low <= high ){ mid = ( low + high )/2; if (arr[mid]== val) return 1; // found! else if (arr[mid] < val) low = mid + 1; else high = mid - 1; } return 0; // not found }

9. Binary Search: binary tree The search divides a list into two small sub-lists till a sub-list is no more divisible. First half First half An entire sorted list First half Second half Second half http://ecomputernotes.com

10. Binary Search Efficiency After 1 bisection N/2 items After 2 bisections N/4 = N/2 2 items . . . After i bisections N/2 i = 1 item i = log 2 N http://ecomputernotes.com

11. Implementation 3: linked list TableNodes are again stored consecutively (unsorted or sorted) insert : add to front; (1 or n for a sorted list ) find : search through potentially all the keys, one at a time; ( n for unsorted or for a sorted list remove : find, remove using pointer alterations; ( n ) key entry and so on http://ecomputernotes.com

12. Implementation 4: Skip List Overcome basic limitations of previous lists Search and update require linear time Fast Searching of Sorted Chain Provide alternative to BST (binary search trees) and related tree structures. Balancing can be expensive. Relatively recent data structure: Bill Pugh proposed it in 1990. http://ecomputernotes.com

13. Skip List Representation Can do better than n comparisons to find element in chain of length n 20 30 40 50 60 head tail http://ecomputernotes.com

14. Skip List Representation Example: n/2 + 1 if we keep pointer to middle element 20 30 40 50 60 head tail http://ecomputernotes.com

15. Higher Level Chains For general n, level 0 chain includes all elements level 1 every other element, level 2 chain every fourth, etc. level i , every 2 i th element 40 50 60 head tail 20 30 26 57 level 1&2 chains http://ecomputernotes.com

16. Higher Level Chains Skip list contains a hierarchy of chains In general level i contains a subset of elements in level i-1 40 50 60 head tail 20 30 26 57 level 1&2 chains http://ecomputernotes.com

17. Skip List: formally A skip list for a set S of distinct (key, element) items is a series of lists S 0 , S 1 , … , S h such that Each list S i contains the special keys  and  List S 0 contains the keys of S in nondecreasing order Each list is a subsequence of the previous one, i.e., S 0  S 1  …  S h List S h contains only the two special keys